Tutorial Exercises

Solution file

Getting Started

To solve exercises of a particular topic, start by carefully reading the exercise tasks. For instance, the tutorial exercises above contain the following three tasks:

\begin{enumerate}[label=\alph*)] \item a) "Give a deterministic finite automaton (DFA) $d_1$ recognizing the language of the regular expression $a + b$.'' \item b) "Give a non-deterministic finite automaton (NFA) $n_1$ recognizing the language of the regular expression $a^{*}$.'' \item c) "Give a regular expression $r_1$ recognizing the language $\{ w \in {\{ a, b \}}{}^* \ \vert\ |w|_b$ is even and $w$ does not end with a $b$ $\}$.'' \end{enumerate}

There are essentially two things to know about how to write your solutions:

your solutions should be named and their name should match exactly the indicated name in the corresponding task.

your solutions must respect the syntax of finite state automata and regular expressions.

Whether your solution is a DFA, a NFA, or a regular expression, giving it a name follows the same syntax:

let 'name' = 'your solution'
For instance, the names of solutions for the three tasks above must be d1, n1, and r1 respectively, and the submission file for the tutorial exercises should look like
let d1 = ...
let n1 = ...
let r1 = ...

Let's see now how to write down the solutions themselves.

Syntax of Finite State Automata

A finite state automaton consists of a set of states and a set of labelled transitions between two given states introduced respectively by the following keywords with colon ":" sign :
states:
...
delta:
...
A state is declared by an alphanumerical ([a-z A-Z 0-9]+) identifier followed by a semicolon ";". Each automaton should have exactly one initial state and zero or more final states. The initial state is marked by "-->" sign and by "<->" sign if it is also final. A final state is marked by "<--" sign.
A labelled transition between two given states q1 and q2 consists of a triplet
q1 'label-option' q2;
where 'label-option' is either an alphanumerical ([a-z A-Z 0-9]) character identifier or a blank space. The latter case corresponds to the $\lambda$- transition (empty word transition).
With these notations, the automaton d1 can be written as

let d1 =
states:
-->q1;
<--q2;
q3;
delta:
q1 a q2;
q1 b q2;
q2 a q3;
q2 b q3;
q3 a q3;
q3 b q3;

d1new

and the automaton n1 as

let n1 =
states:
<->q1; q2; q3;
delta:
q1 q2;
q2 a q3;
q3 q1;

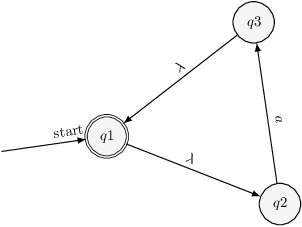
n1new

The images on the right correspond to how your solutions will be printed. You can test it yourself by copy-pasting the definition of d1 or n1 in the drawing window.
The rendering of the automata done automatically, using Graphviz and dot2tex tools. Besides this automated rendering (set default if no decoration of node positionning is detected), AutoMate offers several options for manual positionning of nodes and rendering transitions. See more about those printing options below.

Syntax of Regular Expressions

Let's write now a regular expression r1 to solve the last task.
Each regular expression should be declared as follows:

regexp "r" ;

where regexp is a keyword and r is the proper regular expression written within the string quotes. The syntax of regular expressions consists in the following notations:

\begin{enumerate} \item- $r_i + r_j$, $r_ir_j$ denote union and concatenation of two regular of expressions $r_i$ and $r_j$ respectively; \item- $a, b, 0, 1, ...$ denote each the set containing only the character $a$, $b$, $0$, $1$, ... respectively; \item- $(r_i){}^*$ denotes Kleene star; \item- & denotes an empty word; \item- @ denotes an empty set.

The notations above are mostly standard, apart from those for empty words and empty sets. The conventions for parentheses and precedences of the operators are standard as well. With these notations, we can define r1 as follows:

let r1 = regexp "(a + a*ba*ba*)* + &";
which will be printed in the correction output file as a string

$"(a + a^*ba^*ba^*){}^* + \mathbf{1}"$.

You can now submit the solution file to see how the correction output looks like.

Correction Feedback

Currently, AutoMate gives you a feedback of three different types of exercises:

language modelling	shows why the solution is not equivalent to the exercise's language by gives examples of words showing that: either the submitted solution is either not strong enough and/or that it is is too strong
determinisation	shows one or several of the three different sources of non-determinism: an epsilon transition a pair of transition from the same state and label to two different states a missing transition that causes incompleteness
minimisation	gives a list of states that are distinct in the submitted solution, but should be language-equivalent.

Drawing options for Finite State Automata

Positionning of States

There are two ways of specifying the position of a state during its declaration:

q1[> q2]; will position the state q1 4cm on the right of the previously declared state q2.
[v q2];, [^ q2];, [< q2]; will have a similar effect with below, above, and left direction respectively;

q1[q2 "x" "y"]; will position the state q1 x cm horizontally and y cm vertically with respect to the position of the previously declared state q2. The numerical values x and y should be either integers or floats, eg. "2", "3.5", "0", "-2", ...

For instance, we can draw the automaton n1 more nicely, by positionning states in a triangle as follows:

let n1 =
states:
<->q1;
q2[q1 "5" "0"];
q3[q1 "2.5" "-3"];
delta:
q1 q2;
q2 a q3;
q3 q1;

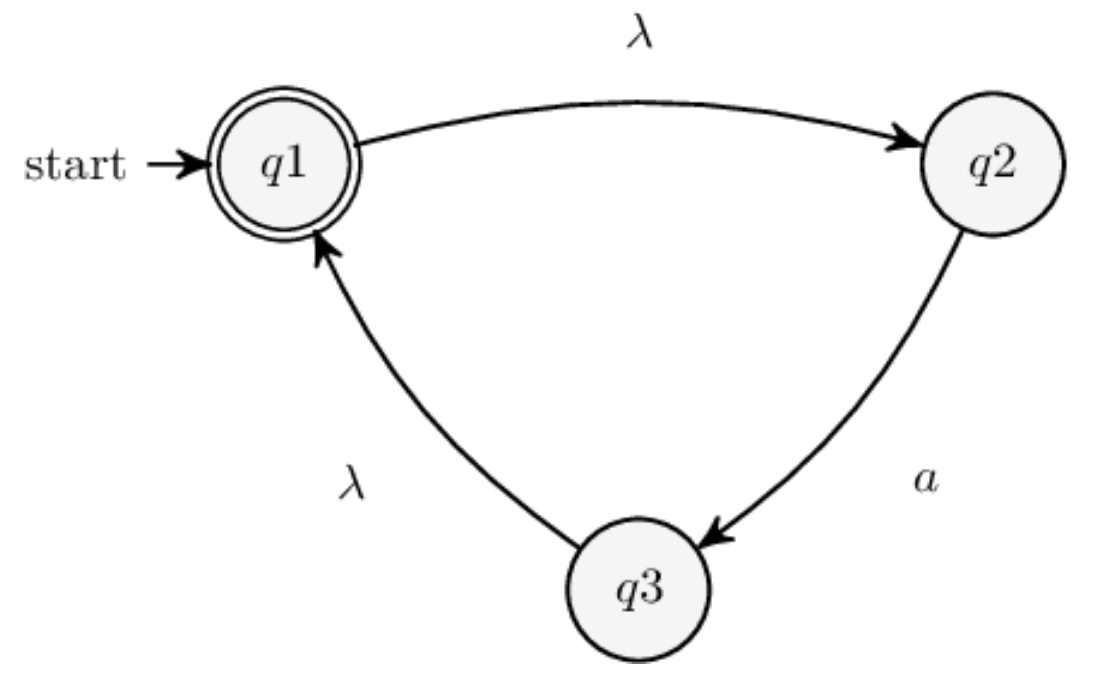
Appearance of Transitions

By default, the arrow of a transition qx a qy; has a slightly bent shape. To make the arrow straight, add [-] in the end of transition declaration eg., qx a qy [-]; . If you have declared sevaral transitions with the same source and destination, all labels will be printed on the same arrow, and it is the first declaration that will determine its shape.